The solution to the system is
 and
and
 . This is obtained by eliminating y through equation manipulation, leading to a unique solution.
. This is obtained by eliminating y through equation manipulation, leading to a unique solution.
To solve the system of equations 5x = 4y + 8 and 3x + 3y = -3, we can use the substitution or elimination method. Let's use elimination:
1. Multiply the second equation by 4 to make the coefficients of y in both equations equal:
5x = 4y + 8
12x + 12y = -12
2. Subtract the first equation from the modified second equation to eliminate y:
(12x + 12y) - (5x = 4y + 8)
7x = -20
3. Solve for x:
 .
.
4. Substitute x back into one of the original equations, let's use the first one:
![\[ 5\left(-(20)/(7)\right) = 4y + 8 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/p598i91xic4zmv4enliao5h2prlsbs7a6f.png)
5. Solve for y:
 .
.
So, the solution to the system of equations is
 and
and
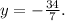
Que. Find Linear equations with two unknowns
5x=4y+8 and 3x+3y=-3