Question

The Statistical Abstract of the United States reported that the average cost per day of owning an automobile in the United states is $7.62. This includes the cost of the car, general maintenance, gasoline, and insurance. A researcher claims that college students' average daily ownership expenses are less than the national average. A random sample of 54 college students who own cars found the average cost per day to be $6.78 with standard deviation $1.77. Use a 5% level of significance to test the claim that a college student's average daily ownership expenses are less than the national average. State the Null and Alternate Hypotheses, calculate the test statistic, compute the P value for this test, state the alpha value, then state your conclusion. Is there enough evidence to support the claim?

Answer 1

Explanation:

The null and the alternative can be computed as:

`H_o : \mu = 7.62`

`H_1 : \mu < 7.62`

`Claim: \mu < 7.62`

`\alpha= 0.05`

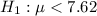
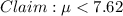
The critical value for a left-tailed test at
`\alpha= 0.05` = -1.645

The test statistics can be computed as:

`Z = (\overline x - \mu)/((\sigma)/(√(n)) )`

`Z = (6.78 - 7.62)/((1.77)/(√(54)) )`

`Z = -3.487`

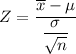
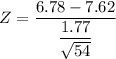
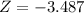
The P-value = (Z< -3.487)

The P-value = 0.00024

Decision Rule: TO reject
`\mathbf{H_o}` at
`\alpha= 0.05`, if test statistics is less than the critical value (left tailed)

Conclusion: We reject
`\mathbf{H_o}` at ∝ = 5%, thus there is enough evidence to support the claim that the college students average daily ownership expenses are less than the national average.