Answer:
Explanation:
The null and the alternative can be computed as:
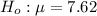
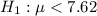
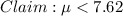
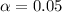
The critical value for a left-tailed test at
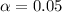 = -1.645
= -1.645
The test statistics can be computed as:
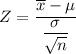
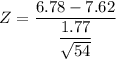
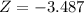
The P-value = (Z< -3.487)
The P-value = 0.00024
Decision Rule: TO reject
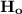 at
at
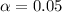 , if test statistics is less than the critical value (left tailed)
, if test statistics is less than the critical value (left tailed)
Conclusion: We reject
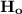 at ∝ = 5%, thus there is enough evidence to support the claim that the college students average daily ownership expenses are less than the national average.
at ∝ = 5%, thus there is enough evidence to support the claim that the college students average daily ownership expenses are less than the national average.