Question

The equation r(t)= (3t+9)i+(sqrt(2)t)j+(t^2)k is the position of a particle in space at time t. Find the angle between the velocity and acceleration vectors at time t=0. What is the angle?

Answer 1

θ = 90º

Step-by-step explanation:

The velocity is given by

v =
`(dr)/(dt)`

calculate

v = 3 i ^ + √2 j ^ + 2t k ^

acceleration is defined by

a = dv / dt

a = 2 k ^

one way to find the angle is with the dot product

v. a = | v | | a | cos θ

cos θ= v.a / | v | | a |

Let's look for the value of each term

v. a = 4 t

| v | =
`√(3^2 + 2 + (2t)^2 )` =
`√( 11 + 4t^2)`

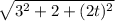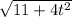
| a | = 2

they ask us for the angle for time t = 0

v. a = 0

| v | = √11 = 3.317

we substitute

cos θ = 0 /√11

cos θ = 0

therefore the angles must be θ = 90º