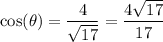Answer:
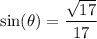
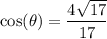
Explanation:
We want to find sin(θ) and cos(θ) given that tan(θ) = 1/4 and sin(θ) > 0.
First, since tan(θ) and sin(θ) are both positive, cos(θ) must be positive as well.
Recall that tangent is the ratio of the opposite side to the adjacent side.
Therefore, the hypotenuse is:
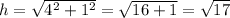
So, with respect to θ, the opposite side is 1, the adjacent is 4, and the hypotenuse is √17.
Then it follows that:
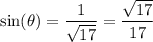
And that: