Answer:
See Explanation
Explanation:
The question has missing details as no link is provided to the "question 3".
However, I'll give a worked solution on how to calculate the equation of a regression line.
Using the following data:
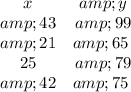
Calculate the equation of the regression line.
The equation is calculated using:

Where:
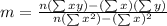
and

So, first we fill in the table with columns x^2, y^2 and xy

From the above table.
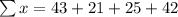
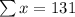
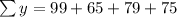
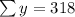
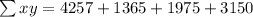
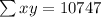

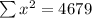
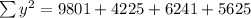
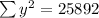
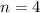
Solving for m
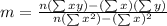

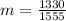
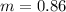 --- approximated
--- approximated
Solving for b

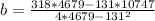
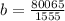
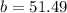
The equation becomes:

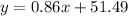
Apply the above steps and you will arrive at a solution.