Answer:
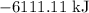
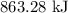
Step-by-step explanation:
m = Mass of automobile = 1100 kg
v = Velocity of car = 120 km/h =

h = Height of hill = 80 m
g = Acceleration due to gravity =
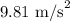
Change in kinetic energy
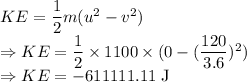
Change in kinetic energy is
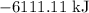
Change in potential energy is given by
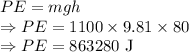
The change in potential energy is
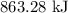 .
.