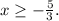The composition f(g(x)) is given by
 , with the restriction that
, with the restriction that
 to ensure the expression inside the square root is non-negative, thereby defining the domain.
to ensure the expression inside the square root is non-negative, thereby defining the domain.
Assuming you want to find the composition f(g(x)), where
 and g(x) = 3x + 5, you can proceed as follows:
and g(x) = 3x + 5, you can proceed as follows:
![\[ f(g(x)) = √(4(3x + 5)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/othv586fcjwpt7cswq5cqn3w371uoht464.png)
Now, simplify the expression inside the square root:
![\[ f(g(x)) = √(12x + 20) \]](https://img.qammunity.org/2024/formulas/mathematics/college/73sca2qd9lhuw8leqhwioj2dxalzf7i0g1.png)
To find any restrictions on the domain, note that the expression inside the square root (12x + 20) must be non-negative for the function to be defined. Therefore, solve the inequality:
![\[ 12x + 20 \geq 0 \]](https://img.qammunity.org/2024/formulas/mathematics/college/g7cad9m74mmv8trzbpvlac8f040vha5kf6.png)
![\[ 12x \geq -20 \]](https://img.qammunity.org/2024/formulas/mathematics/college/itbs8welsdh84olsahmrsaiqn9c3mw7f09.png)
![\[ x \geq -(5)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/college/o36vyxcttm4ipypm1kkm6wnx1eodmp08qj.png)
So, the composition
 is defined for
is defined for