Question

11. In rhombus MATH, MS = 6 and SA = 8. Find the perimeter of the rhombus.

M
А
8
A
S
I
T

Answer 1

40

Explanation:

A rhombus diagonals form perpendicular angles. It also bisects and form 4 right triangles. Looking at triangle MAS, we can use pythagorean theorem to find the side MA.

`ms {}^(2) + sa {}^(2) = {ma}^(2)`

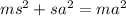
ms=6, sa =8 so we plug that in.

`6 {}^(2) + {8}^(2) = ma {}^(2)`

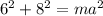
Simplify

`36 + 64 = ma {}^(2)`

`100 = ma {}^(2)`

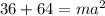
take sqr root

`√(100) = ma`

`ma = 10`

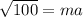
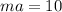
Now let find the perimeter

Since perimeter of a Rhombus is 4a where a is the length of a side. We plug it in

`4(10) = 40`

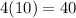
The answer is 40