Question

Suppose that A and B are two events in a sample space, S, which are independent and which have equal probability, p, of occurring. Suppose further that the probability that neither A nor B occurs is 0.81. Find the probability that both A and B occur.

Answer 1

The probability that both A and B occur is P = 0.01

Explanation:

Both events A and B have a probability p of occurring.

Then both events A and B have a probability (1 - p) of NOT occurring.

The probability that neither A or B occurs is equal to the product of the individual probabilities, and this is equal to 0.81, then:

(1 - p)*(1 - p) = 0.81

1 - 2*p + p^2 = 0.81

p^2 - 2*p + 0.19 = 0

We can solve this if we use Bhaskara's equation, the two solutions are:

`p = (-(-2) +- √((-2)^2 - 4*1*0.19) )/(2*1) = (2 + - 1.8)/(2)`

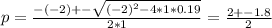
Then the two solutions are:

p = (2 + 1.8)/2 = 3.8/2 = 1.9

A probability must be a number between zero and one, and this is larger than one, so this solution can be discarded.

the other solution is:

p = (2 - 1.8)/2 = 0.2/2 = 0.1

This means that the probability that event A occurs is p = 0.1

And the probability that event B occurs is p = 0.1

The probability that both events occur is equal to the product of the individual probabilities, which is:

P = 0.1*0.1 = 0.01