Question

The dimensions of a garden are shown. write an expression to find the perimeter

Answer 1

The perimeter of the garden with a width of
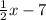`\( (1)/(2)x - 7 \)` and a length of x , substitute these values into the formula
`\( 2 * (3x - 7/2)` , yielding
3x - 7/2 .

Certainly, let's break down the steps for calculating the perimeter of the garden:

1. Given Information:

- Width of the garden:
`\( (1)/(2)x - 7 \)`

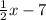
- Length of the garden: x

2. Perimeter Formula:

- The formula for the perimeter P of a rectangle is
`\( P = 2 * (\text{Length} + \text{Width}) \).`

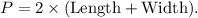
3. Substitute Width and Length:

- Substitute the expressions for width and length into the perimeter formula:

`\[ P = 2 * \left(x + (1)/(2)x - 7\right) \]`

4. Combine Like Terms:

- Simplify the expression inside the parentheses:

`\[ P = 2 * \left((3)/(2)x - 7\right) \]`

5. Distribute the 2:

- Distribute the 2 to both terms inside the parentheses:

`\[ P = 2 * (3)/(2)x - 2 * 7 \]`

P = 3x - 14

6. Final Result:

- The perimeter of the garden is
`\( 3x - (7)/(2) \)`.

The step-by-step calculation demonstrates how to substitute the given expressions into the perimeter formula and simplify the resulting expression for the specific case of the garden's dimensions.