Final Answer:
You would need to be approximately 528 meters away from the Eiffel Tower to capture its entire length in a photograph using a cheap cell phone camera with a single lens.
Step-by-step explanation:
To determine the distance required to capture the entire length of the Eiffel Tower in a photo, we can use the thin lens formula:
![\[ (1)/(f) = (1)/(d_o) + (1)/(d_i) \]](https://img.qammunity.org/2024/formulas/physics/high-school/l4mx0hbwqvoq9zbnxbztge1g7edxl72rpg.png)
Given:
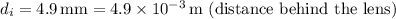
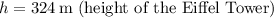
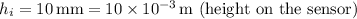
First, find the magnification produced by the lens:
![\[ \text{Magnification} = (h_i)/(h) \]](https://img.qammunity.org/2024/formulas/physics/high-school/5mn8h12rsj5etpdnkbet7rnx60leieizt3.png)
![\[ \text{Magnification} = (10 * 10^(-3))/(324) = 3.086 * 10^(-5) \]](https://img.qammunity.org/2024/formulas/physics/high-school/56mh82qh31y51jpe0pj2ot3t9hfehvy566.png)
Now, calculate the image distance from the lens using the magnification formula:
![\[ \text{Magnification} = (d_i)/(d_o) \]](https://img.qammunity.org/2024/formulas/physics/high-school/g39ux1az1owysyfwl5deyb8i8nm2qv2cfe.png)
![\[ d_o = \frac{d_i}{\text{Magnification}} = (4.9 * 10^(-3))/(3.086 * 10^(-5)) \approx 158.85 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/5kf21zmqph0jilgyc4xur3skxset4lt0n9.png)
To capture the entire height of the Tower on the sensor, the object distance should be the sum of the tower's height and the distance behind the lens:
![\[ d_o = d_i + h \]](https://img.qammunity.org/2024/formulas/physics/high-school/ybz4ob8ll41u3mwvqbm3j9kf9tlkrk8ari.png)
![\[ 158.85 \, \text{m} = 4.9 \, \text{mm} + h \]](https://img.qammunity.org/2024/formulas/physics/high-school/ekf2htewff8c59nnxn4cy8l5po6cwqo7vx.png)
![\[ h = 158.85 \, \text{m} - 4.9 \, \text{mm} \approx 158.85 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/h6qrdo8wgjn6kk00h0mhzfm3stk34rizpm.png)
Therefore, the distance required to capture the entire length of the Eiffel Tower using the cheap cell phone camera would be approximately
