Question

Are the expressions \(8(9-6x+11)\) and \(15+\frac{3}{2}(-32x+120)-35\) equivalent to \(-16(3x-10)\)?

A) Yes, the expressions are equivalent.

B) No, the expressions are not equivalent.

Answer 1

We've simplified each expression, we can clearly see that:
Expression 1:
`\(160 - 48x\)`
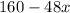
Expression 2:
`\(160 - 48x\)`
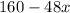
Expression 3:
`\(-48x + 160\)`
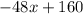
All three expressions are equivalent to one another, since each simplifies to the same combination of terms.
Therefore, the answer is option: A) Yes, the expressions are equivalent.

Let's examine each expression step by step to see if they are equivalent to the given expression
`\(-16(3x-10)\)`.
**Expression 1:
`\(8(9-6x+11)\)`**
Simplify by distributing the 8 across each term inside the parentheses:

`\[8 \cdot 9 - 8 \cdot 6x + 8 \cdot 11 = 72 - 48x + 88\]`
Combine the constant terms:

`\[72 + 88 = 160\]`
Now, the expression is:

`\[160 - 48x\]`

**Expression 2:
`\(15+(3)/(2)(-32x+120)-35\)`**
Before distributing, simplify the constant terms outside the parentheses:

`\[15 - 35 = -20\]`
Now, distribute
`\((3)/(2)\)` across each term inside the parentheses:

`\[(3)/(2) \cdot (-32x) + (3)/(2) \cdot 120 = -48x + 180\]`
Now, the expression is:

`\[180 - 48x - 20\]`
Combine the constant terms:

`\[180 - 20 = 160\]`
So, the second expression becomes:

`\[160 - 48x\]`

**Expression 3:
`\(-16(3x-10)\)`**
Distribute the
`\(-16\)` across each term inside the parentheses:

`\[-16 \cdot 3x + -16 \cdot (-10) = -48x + 160\]`
So, the third expression is:

`\[-48x + 160\]`
Now that we've simplified each expression, we can clearly see that:
Expression 1:
`\(160 - 48x\)`
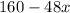
Expression 2:
`\(160 - 48x\)`
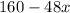
Expression 3:
`\(-48x + 160\)`
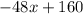
All three expressions are equivalent to one another, since each simplifies to the same combination of terms.
Therefore, the answer is:z
A) Yes, the expressions are equivalent.