Answer:
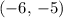 is outside the circle of radius of
is outside the circle of radius of
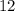 centered at
centered at
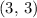 .
.
Explanation:
Let
 and
and
 denote the center and the radius of this circle, respectively. Let
denote the center and the radius of this circle, respectively. Let
 be a point in the plane.
be a point in the plane.
Let
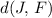 denote the Euclidean distance between point
denote the Euclidean distance between point
 and point
and point
 .
.
In other words, if
 is at
is at
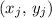 while
while
 is at
is at
 , then
, then
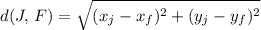 .
.
Point
 would be inside this circle if
would be inside this circle if
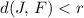 . (In other words, the distance between
. (In other words, the distance between
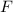 and the center of this circle is smaller than the radius of this circle.)
and the center of this circle is smaller than the radius of this circle.)
Point
 would be on this circle if
would be on this circle if
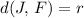 . (In other words, the distance between
. (In other words, the distance between
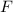 and the center of this circle is exactly equal to the radius of this circle.)
and the center of this circle is exactly equal to the radius of this circle.)
Point
 would be outside this circle if
would be outside this circle if
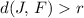 . (In other words, the distance between
. (In other words, the distance between
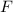 and the center of this circle exceeds the radius of this circle.)
and the center of this circle exceeds the radius of this circle.)
Calculate the actual distance between
 and
and
 :
:
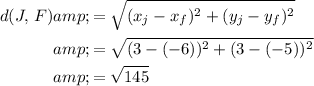 .
.
On the other hand, notice that the radius of this circle,
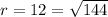 , is smaller than
, is smaller than
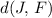 . Therefore, point
. Therefore, point
 would be outside this circle.
would be outside this circle.