Answer:
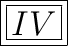
Explanation:
Given:
x>0
Which means
x is any number greater than 0 ig 1,2,3,4,5,7,9.......
y<0
Which means
y Is any number smaller than 0
ig -1,-2,-3,-4,-5.........
So according to the question
The coordinates are
(x,-y)
Therefore,
The points are located to Quadrant IV