Final Answer:
The equation for the absolute value graph is
 and the domain is all real numbers
and the domain is all real numbers
 The range is
The range is
 since the absolute value of any real number is non-negative, and adding 3 ensures that the range starts from 3.
since the absolute value of any real number is non-negative, and adding 3 ensures that the range starts from 3.
Step-by-step explanation:
The given equation
 represents an absolute value function where the expression
represents an absolute value function where the expression
 ensures that the function takes the absolute value of ( x - 2 ). This absolute value function shifts the graph horizontally by 2 units to the right.
ensures that the function takes the absolute value of ( x - 2 ). This absolute value function shifts the graph horizontally by 2 units to the right.
For the domain, since
 is valid for all real numbers, the domain of
is valid for all real numbers, the domain of

The range is determined by the absolute value part, which is always non-negative. Adding 3 to this ensures that the lowest value the function can take is 3. Therefore, the range is
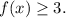
In summary, the equation
 describes an absolute value graph that is defined for all real numbers, and its range starts from 3 and goes upward.
describes an absolute value graph that is defined for all real numbers, and its range starts from 3 and goes upward.