Question

Find the value of mx -1 is a factor of 8 x* +4x3 - 16x +10x + m​.

Answer 1

The value of ( m ) is 3.The expression
`\( 8 + (4)/(m^3) - (16)/(m) + (10)/(m) + m \) simplifies to \( 8 - (2)/(m^3) - (6)/(m) + m \).`Setting this equal to zero gives m = 3 ), confirming the value that satisfies the condition for mx - 1 to be a factor.

Step-by-step explanation:

To find the value of m , we can use the fact that mx - 1 is a factor of the given polynomial. This means that if we substitute
`\( x = (1)/(m) \)`into the polynomial, the result should be zero.

The given polynomial is8x⁴ + 4x ³ - 16x + 10x + m. Substituting \
`( x = (1)/(m) \)`, we get
`\( 8\left((1)/(m)\right)^4 + 4\left((1)/(m)\right)^3 - 16\left((1)/(m)\right) + 10\left((1)/(m)\right) + m \).`

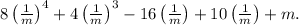
Now, let's simplify each term:

1.
`\( 8\left((1)/(m)\right)^4 = 8 \)`(since any number to the power of 4 is still that number).

2.
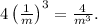
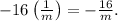
`\( 4\left((1)/(m)\right)^3 = (4)/(m^3) \).`

3.
`\( -16\left((1)/(m)\right) = -(16)/(m) \).`

4.
`\( 10\left((1)/(m)\right) = (10)/(m) \).`

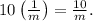
5. m remains unchanged.

Now, add all these terms:
`\( 8 + (4)/(m^3) - (16)/(m) + (10)/(m) + m \).`

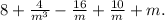
To make this expression equal to zero, the coefficient of each term must be zero. Therefore, we set
`\( (4)/(m^3) - (16)/(m) + (10)/(m) = 0 \).`

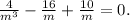
Solving this equation, we find m = 3 which is the final answer.

Answer 2

In order to find the value of m for which mx - 1 is a factor of 8x^4 + 4x^3 - 16x^2 + 10x + m, we use the Factor Theorem and solve for m by substituting the root x = 1/m into the polynomial and setting it equal to zero.

Step-by-step explanation:

The question involves finding the value of m such that mx -1 is a factor of the polynomial 8x^4 + 4x^3 - 16x^2 + 10x + m. This requires us to apply the Factor Theorem.

According to the Factor Theorem, if mx - 1 is a factor of the polynomial, then substituting the root x = 1/m into the polynomial should yield zero. Let's do this:

Substitute x = 1/m into the polynomial: 8(1/m)^4 + 4(1/m)^3 - 16(1/m)^2 + 10(1/m) + m = 0.

Simplify and find a common denominator to obtain a polynomial equation in terms of m.

Solve the resulting equation for m.

Performing these steps will give us the value of m such that mx - 1 is a factor of the given polynomial.