Final Answer:
The length of the diameter between points P(-1,3) and Q(5,-1) is 10 units.
Step-by-step explanation:
To find the length of the diameter, we can use the distance formula in coordinate geometry. The distance formula between two points
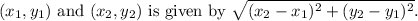
In this case, the coordinates of points P and Q are
 respectively. Applying the distance formula:
respectively. Applying the distance formula:
![\[d = √((5 - (-1))^2 + (-1 - 3)^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bbx6cj47gcyiuhi0d4ytbv6vf793srct35.png)
![\[d = √(6^2 + (-4)^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1f7ensm4d2fonx6c6t7h2vvzgdr6thmrkv.png)
![\[d = √(36 + 16)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ez21wrr7swq1wert248kcah9qnl9y0wsjd.png)
![\[d = √(52)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qm2fgc2qgdk0n8tmzo0tuwtcymg3r8drbs.png)
![\[d = 2√(13)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rzr5v02ni7w3kxpb44zrwun1zr7pt0f4p3.png)
Hence, the length of the diameter, which is the distance between points P and Q, is
 units. To simplify further,
units. To simplify further,
 equals
equals
 , which ultimately simplifies to
, which ultimately simplifies to
 units.
units.