Question

Mrs. Grubb bought some shirts for $4 each and some hats for $12 each. She bought 9 pieces of clothing for $100. Write a system of equations that you could use to solve this problem.

Answer 1

Mrs. grub bought total number of shirts = 1

Mrs. grub bought total number of hats = 8

Explanation:

Let Mrs. grub bought total number of shirts = x

Let Mrs. grub bought total number of hats = y

As given,

Price of 1 shirt = $4

Price of 1 hat = $12

⇒ Price of x shirts = $ 4x

Price of y hats = $ 12y

Given that,

Mrs. Grubb bought total piece of clothes = 9

⇒ x + y = 9 .......(1)

Also given,

She bought all clothing for $100

⇒ 4x + 12 y = 100 ........(2)

Divide equation (2) by 4 we get

x + 3y = 25 .......(3)

Now,

Subtract equation (1) from equation (3) , we get

x + 3y - ( x + y ) = 25 - 9

⇒ x + 3y - x - y = 16

⇒2y = 16

⇒y =
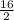`(16)/(2)` = 8

⇒ y = 8

Put value of y in equation (3), we get

x + 3(8) = 25

⇒x + 24 = 25

⇒x = 25 - 24 = 1

⇒x = 1

∴ we get

Mrs. grub bought total number of shirts = x = 1

Mrs. grub bought total number of hats = y = 8