Question

a total of 42 men have served as president through 2010. if 43 men were selected at random, find the probability that at least 2 men will have the same birthday

Answer 1

The probability that at least 2 men will have the same birthday is approximately 1.

Let's find the probability that at least 2 men will have the same birthday.

We can use the complement approach, which involves calculating the probability of the event's opposite (all 43 men having different birthdays) and subtracting it from 1.

The probability of all 43 men having different birthdays is:

`\binom{42}{43} \cdot (365!)/((365-43)!)`

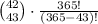
where:

( 42/43 ) is the binomial coefficient, which represents the number of ways to choose 43 men out of 42

365!/ (365−43)!

is the number of ways to arrange the birthdays of the 43 men, assuming no birthdays are the same

The probability of at least 2 men having the same birthday is then:

`1-\binom{42}{43} \cdot (365!)/((365-43)!)`

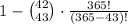
Evaluating this expression, we get:

`1-0 \approx 1`

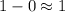
Therefore, the probability that at least 2 men will have the same birthday is approximately 1.