Question

What point on the line y=7x+10 is closest to the origin?

A) (-2, 4)
B) (-1, 3)
C) (0, 10)
D) (1, 17)

Answer 1

The point on the line y = 7x + 10 closest to the origin is option B) (-1, 3).

Step-by-step explanation:

To find the point on the line closest to the origin, we can use the distance formula
`\(d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)\)` . In this case, the coordinates of the origin are O(0, 0), and we need to find the distance from O to each of the given points.

Let's calculate the distances:

1. For point A (-2, 4):
`\(d_A = √((-2 - 0)^2 + (4 - 0)^2) = √(4 + 16) = √(20)\).`

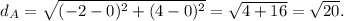
2. For point B (-1, 3):
`\(d_B = √((-1 - 0)^2 + (3 - 0)^2) = √(1 + 9) = √(10)\).`

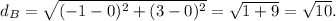
3. For point C (0, 10):
`\(d_C = √((0 - 0)^2 + (10 - 0)^2) = √(100) = 10\).`

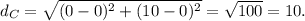
4. For point D (1, 17):
`\(d_D = √((1 - 0)^2 + (17 - 0)^2) = √(1 + 289) = √(290)\).`

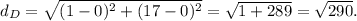
The smallest distance is
`\(√(10)\)`, which corresponds to option B (-1, 3). Therefore, the point (b)(-1, 3) on the line y = 7x + 10 is closest to the origin.