Answer:
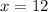
Explanation:
Method 1: Pythagorean Theorem
We can use the Pythagorean Theorem to solve for
 . The Pythagorean Theorem states that in a right triangle, the sum of the squares of the legs' side lengths is equal to the length of the hypotenuse squared. Simply put,
. The Pythagorean Theorem states that in a right triangle, the sum of the squares of the legs' side lengths is equal to the length of the hypotenuse squared. Simply put,
 , where
, where
 and
and
 are the legs and
are the legs and
 is the hypotenuse. In this case, we know that
is the hypotenuse. In this case, we know that
 ,
,
 , and
, and
 , so we get:
, so we get:

 (Substitute
(Substitute
 ,
,
 , and
, and
 into
into
 )
)
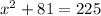 (Simplify exponents)
(Simplify exponents)
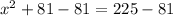 (Subtract
(Subtract
 from both sides of the equation to isolate
from both sides of the equation to isolate
 )
)
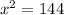 (Simplify)
(Simplify)
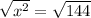 (Take the square root of both sides)
(Take the square root of both sides)
 (Simplify, remember that each positive number has two square roots: a positive one and a negative one)
(Simplify, remember that each positive number has two square roots: a positive one and a negative one)
In the context of the situation, we know that
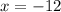 is an extraneous solution because a polygon cannot have negative side lengths. Therefore, the final answer is
is an extraneous solution because a polygon cannot have negative side lengths. Therefore, the final answer is
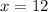 .
.
Method 2: Pythagorean Triples
Method 1 works, but there's an easier way to find the value of
 . If we look at the given lengths of
. If we look at the given lengths of
 and
and
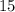 , we can observe that this triangle is a
, we can observe that this triangle is a
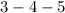 right triangle enlarged by a scale factor of
right triangle enlarged by a scale factor of
 , because
, because
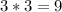 and
and
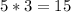 . The only side length that's missing is the
. The only side length that's missing is the
 . Therefore,
. Therefore,
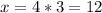 . Hope this helps!
. Hope this helps!