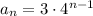Question

This math my graduation depends on it

Answer 1

In an arithmetic sequence, consecutive terms have a fixed distance d between them. If a₁ is the first term, then

2nd term = a₂ = a₁ + d

3rd term = a₃ = a₂ + d = a₁ + 2d

4th term = a₄ = a₃ + d = a₁ + 3d

and so on, up to

nth term =
`a_n = a_(n-1) + d = a_(n-2) + 2d = a_(n-3) + 3d = \cdots = a_1 + (n-1)d`

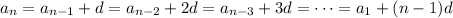
so that every term in the sequence can be expressed in terms of a₁ and d.

6. It's kind of hard to tell, but it looks like you're given a₁₃ = -53 and a₃₅ = -163.

We have

a₁₃ = a₁ + 12d = -53

a₃₅ = a₁ + 34d = -163

Solve for a₁ and d. Eliminating a₁ and solving for d gives

(a₁ + 12d) - (a₁ + 34d) = -53 - (-163)

-22d = 110

d = -5

and solving for a₁, we get

a₁ + 12•(-5) = -53

a₁ - 60 = -53

a₁ = 7

Then the nth term is recursively given by

`a_n = a_(n-1)-5`

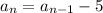
and explicitly by

`a_n = 7 + (n-1)(-5) = 12 - 5n`

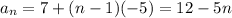
7. We do the same thing here. Use the known terms to find a₁ and d :

a₁₉ = a₁ + 18d = 15

a₃₈ = a₁ + 37d = 72

⇒ (a₁ + 18d) - (a₁ + 37d) = 15 - 72

⇒ -19d = -57

⇒ d = 3

⇒ a₁ + 18•3 = 15

⇒ a₁ = -39

Then the nth term is recursively obtained by

`a_n = a_(n-1)+3`

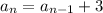
and explicitly by

`a_n = -39 + (n-1)\cdot3 = 3n-42`

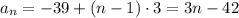
8. I won't both reproducing the info I included in my answer to your other question about geometric sequences.

We're given that the 1st term is 3 and the 2nd term is 12, so the ratio is r = 12/3 = 4.

Then the next three terms in the sequence are

192 • 4 = 768

768 • 4 = 3072

3072 • 4 = 12,288

The recursive rule with a₁ = 3 and r = 4 is

`a_n = 4a_(n-1)`

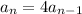
and the explicit rule would be

`a_n = 3\cdot4^(n-1)`