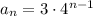In an arithmetic sequence, consecutive terms have a fixed distance d between them. If a₁ is the first term, then
2nd term = a₂ = a₁ + d
3rd term = a₃ = a₂ + d = a₁ + 2d
4th term = a₄ = a₃ + d = a₁ + 3d
and so on, up to
nth term =
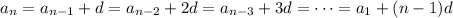
so that every term in the sequence can be expressed in terms of a₁ and d.
6. It's kind of hard to tell, but it looks like you're given a₁₃ = -53 and a₃₅ = -163.
We have
a₁₃ = a₁ + 12d = -53
a₃₅ = a₁ + 34d = -163
Solve for a₁ and d. Eliminating a₁ and solving for d gives
(a₁ + 12d) - (a₁ + 34d) = -53 - (-163)
-22d = 110
d = -5
and solving for a₁, we get
a₁ + 12•(-5) = -53
a₁ - 60 = -53
a₁ = 7
Then the nth term is recursively given by
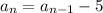
and explicitly by
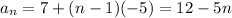
7. We do the same thing here. Use the known terms to find a₁ and d :
a₁₉ = a₁ + 18d = 15
a₃₈ = a₁ + 37d = 72
⇒ (a₁ + 18d) - (a₁ + 37d) = 15 - 72
⇒ -19d = -57
⇒ d = 3
⇒ a₁ + 18•3 = 15
⇒ a₁ = -39
Then the nth term is recursively obtained by
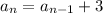
and explicitly by
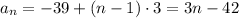
8. I won't both reproducing the info I included in my answer to your other question about geometric sequences.
We're given that the 1st term is 3 and the 2nd term is 12, so the ratio is r = 12/3 = 4.
Then the next three terms in the sequence are
192 • 4 = 768
768 • 4 = 3072
3072 • 4 = 12,288
The recursive rule with a₁ = 3 and r = 4 is
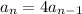
and the explicit rule would be