Answer:
B. 29º
Explanation:
Given that BCDE is a parallelogram, then
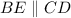 and A, E and D are collinear. Then, angle E inside triangle ABE and angle D inside parallelogram BCDE have the same measure. That is:
and A, E and D are collinear. Then, angle E inside triangle ABE and angle D inside parallelogram BCDE have the same measure. That is:
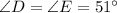 (1)
(1)
In addition, the sum of internal angles in triangles equals 180º, which implies that:
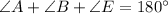 (2)
(2)
If we know that
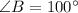 and
and
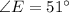 , then
, then
 is:
is:


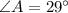
Hence, correct answer is B.