Question

The repair time for air conditioning units is believed to have a normal distribution with a mean of 38 minutes. What is the standard deviation of repair time if 40% of the units are repaired between 33 and 43 minutes

Answer 1

The standard deviation of air conditioning unit repair time is approximately determined as the interval between 33 and 43 minutes, where 40% of units are repaired. Calculations, based on z-scores and the given percentiles, yield a standard deviation of approximately 5 minutes for the repair time distribution with a mean of 38 minutes.

Step-by-step explanation:

To find the standard deviation of repair time, we need to use the concept of z-scores in a standard normal distribution.

Let's denote the mean repair time as
`\( \mu = 38 \)` minutes.

We know that 40% of the units are repaired between 33 and 43 minutes. This interval corresponds to the range
`\( \mu - x \)` to
`\( \mu + x \)`, where
`\( x \)` is the standard deviation.

First, let's find the z-scores corresponding to the given percentiles in a standard normal distribution:

1. For the lower bound (33 minutes):

`\[ z_{\text{lower}} = (33 - \mu)/(\sigma) \]`

2. For the upper bound (43 minutes):

`\[ z_{\text{upper}} = (43 - \mu)/(\sigma) \]`

Now, we know that the area between these z-scores is 40%. Using a standard normal distribution table or calculator, we can find the z-scores that correspond to cumulative probabilities.

Let's assume
`\( z_{\text{lower}} \)` corresponds to the 20th percentile and
`\( z_{\text{upper}} \)` corresponds to the 60th percentile (since the area between them is 40%).

Now, we can solve for
`\( \sigma \)` using the z-scores:

`\( z_{\text{lower}} = (33 - \mu)/(\sigma) \\\( z_{\text{upper}} = (43 - \mu)/(\sigma) \\`

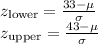
Plug in the values and solve for
`\( \sigma \)`.

`\( (33 - \mu)/(\sigma) = z_{\text{lower}} \\\( (43 - \mu)/(\sigma) = z_{\text{upper}} \\`

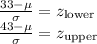
Substitute
`\( \mu = 38 \)` and the values of
`\( z_{\text{lower}} \)` and
`\( z_{\text{upper}} \)` to find
`\( \sigma \)`. Once you find
`\( \sigma \)`, that will be the standard deviation of the repair time.