Final Answer:
![\[ y(0.1) \approx 0.78032, \quad y(0.2) \approx 0.62426, \quad y(0.3) \approx 0.49941, \quad y(0.4) \approx 0.39953 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u2yewdccn16qd9l8c1dyhtu84lfami1n75.png)
Step-by-step explanation:
To approximate the solution using the Euler method, we start with the given initial value problem \
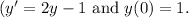 The Euler method involves using the formula
The Euler method involves using the formula
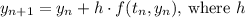 is the step size,
is the step size,
 is the derivative at the current point, and
is the derivative at the current point, and
 is the current value of the solution.
is the current value of the solution.
Given
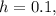 we can iteratively calculate the values of
we can iteratively calculate the values of
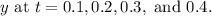 Starting with
Starting with
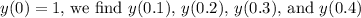 using the Euler method.
using the Euler method.
The detailed calculations involve evaluating
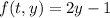 at each step and updating
at each step and updating
 accordingly. For example, to find
accordingly. For example, to find
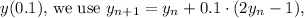 and similarly for the subsequent values. The rounded results are presented in the final answer.
and similarly for the subsequent values. The rounded results are presented in the final answer.
These approximations demonstrate the progression of the solution over the given time intervals, providing a numerical insight into how the function evolves according to the given initial value problem and Euler method.