Answer:
80 rooms
Explanation:
Given: 70 of the rooms in a hotel are full such that the hotel is 87.5% full.
To find: total number of rooms in the hotel
Solution:
Number of filled rooms
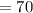
Percentage if filled rooms

Let
 denotes total number of rooms.
denotes total number of rooms.
Therefore,

So, there are
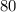 rooms in the hotel.
rooms in the hotel.