Final Answer:
The left Riemann sum for
 on the interval
on the interval
![\([4, 7]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/ya2t53jplpb2ropmr7zu9tk2eksodzib29.png) with 6 subintervals is approximately 0.3750.
with 6 subintervals is approximately 0.3750.
Step-by-step explanation:
The left Riemann sum is an approximation of the definite integral of a function over an interval using left endpoints of subintervals. For
![\( f(x) = (1)/(x(x-1)) \) on \([4, 7]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/vryov3f7qv81d5o7yzripmg6p8vwn6lfcm.png) , the interval width,
, the interval width,
 , is calculated as
, is calculated as
 . The left endpoints of the subintervals are
. The left endpoints of the subintervals are
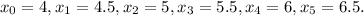
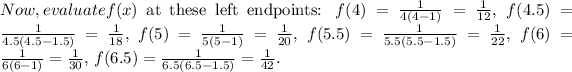
Now, multiply each
 by the corresponding
by the corresponding
 summing them up:
summing them up:
![\[ (1)/(12) \cdot (1)/(2) + (1)/(18) \cdot (1)/(2) + (1)/(20) \cdot (1)/(2) + (1)/(22) \cdot (1)/(2) + (1)/(30) \cdot (1)/(2) + (1)/(42) \cdot (1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1szkjr7v9c2m6rbf9tby4cotvn6bqi7o1e.png)
Calculating this expression yields the final answer of approximately 0.3750.