Question

Question undefined

Suppose that 3100 is borrowed for four years at an interest rate of 2% per year, compounded continuously. Find the amount owed, assuming no payments are made until the end.

Answer 1

The amount owed after four years, assuming continuous compounding, is approximately $3357.65.

To solve this problem

We can use the formula for continuous compound interest:

`A = P * e^(^r^t^)`

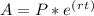
Where:

• A is the total debt after t years.
• P is equal to the principal, or the whole amount borrowed.
• e is equal to Euler's number, or around 2.71828.
• r is the annual interest rate (given in decimal notation).
• t = the total years

Given:

P = $3100

r = 0.02 (2% expressed as a decimal)

t = 4 years

When we enter the provided values into the formula, we get:

`A = 3100 * e^(^0^.^0^2^*^4^)`

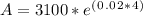
Now, we can calculate the value of
`e^(^0^.^0^2^*^4^)` utilizing a calculator. The result is approximately 1.082085.

Reentering this value into the formula yields the following:

`A = 3100 * 1.082085`

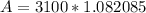
Now, calculating this, we find:

A ≈ $3,357.65

Therefore, the amount owed after four years, assuming continuous compounding, is approximately $3357.65.