Answer:

Explanation:
1) if the point A has coordinates (-1;10) and the point B - (5;2), then it is possible to write common view of the required equation of the line:

2) if to substitute the coordinates of A&B into the common equation, then:
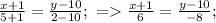
3) finally, in slope-intersection form:
3y= -4x+26; ⇔ y= -4/3 x +26/3.
P.S. the suggested way of the solution is not the only one.