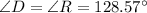Question

The deck that Amos is building is in the shape of a parallelogram, DGRY. The measure of

Answer 1

Complete Question:

The deck that Amos is building is in the shape of a parallelogram, DGRY. The measure of D is five-halves the measure of Y. Find the measure of each angle of the deck.

Answer:

`\angle G = \angle Y = 51.43 ^(\circ)`

`\angle D = \angle R = 128.57 ^(\circ)`

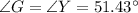
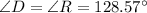
Explanation:

Given

Shape: Parallelogram DGRY

Dimension:
`\angle D = (5)/(2)\angle Y`

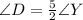
Required

Find the measure of each angle

D and R are opposite sides & G and Y are also opposite sides.

So, we have:

`\angle D = \angle R = (5)/(2)\angle Y`

and

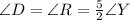
`\angle G = \angle Y`

The sum of angles is given as:

`\angle D + \angle G + \angle R + \angle Y=360^(\circ)`

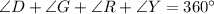
Substitute values for
`\angle D, \angle G \ \& \angle R`

`(5)/(2)\angle Y + (5)/(2)\angle Y + \angle Y + \angle Y = 360^(\circ)`

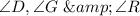
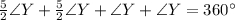
Take LCM

`(5\angle Y + 5\angle Y + 2\angle Y+ 2\angle Y)/(2)= 360^(\circ)`

`(14\angle Y)/(2)= 360^(\circ)`

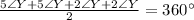
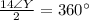
Multiply both sides by
`(2)/(14)`

`(2)/(14) * (14\angle Y)/(2)= 360^(\circ) * (2)/(14)`

`\angle Y= 360^(\circ) * (2)/(14)`

`\angle Y= ( 360^(\circ) *2)/(14)`

`\angle Y= (720^(\circ))/(14)`

`\angle Y= 51.43 ^(\circ)`

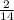
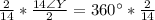
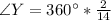
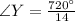
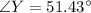
So:

`\angle G = \angle Y = 51.43 ^(\circ)`

`\angle D = (5)/(2)\angle Y`

`\angle D = (5)/(2) * 51.43^(\circ)`

`\angle D = (5* 51.43^(\circ))/(2)`

`\angle D = (257.15^(\circ))/(2)`

`\angle D = 128.57 ^(\circ)`

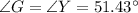
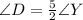
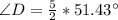
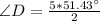
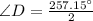
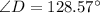
Hence:

`\angle D = \angle R = 128.57 ^(\circ)`