Answer:
Jared did not get the correct answer. The solution to his equation is k = 3, giving 3, 4, and 5 as the three integers. However, 3 and 5 are not even integers. He should have used the equation:
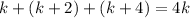 ,
,
which gives us k = 6, and the correct answer 6, 8, and 10.
Explanation:
Jared wanted three consecutive even integers, whose sum is 4 times the first integer.
He let k represent the first integer and wrote:
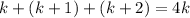
We can solve this first. Combine like terms:
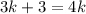
So:
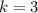
This means that our sequence will be 3, 4, and 5, which is not correct since we have odd integers.
Jared did not get the correct answer. The solution to his equation is k = 3, giving 3, 4, and 5 as the three integers. However, 3 and 5 are not even integers. He should have used the equation*:
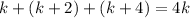 ,
,
which gives us k = 6**, and the correct answer 6, 8 , and 10.
To verify, 6 + 8 + 10 = 24.
And 6(4) = 24, so our answer is correct.
**To solve, we can combine like terms:
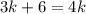
So:
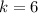
*The reason we use (k + 2) instead of (k + 1) is because (if k is an even number), then adding 2 guarantees another even number. If we added only 1, we will get odd numbers.