Question

What is the value of tangent at (-3/2, 1/2)?
A) -3
B) 1/3
C) 3
D) -1/3

Answer 1

The value of tangent at the point (-3/2, 1/2) is calculated as the ratio of the y-coordinate to the x-coordinate, which is -1/3, corresponding to option D.

Step-by-step explanation:

The value of tangent for a point in the Cartesian coordinate system is determined by the ratio of the y-coordinate to the x-coordinate of the point. For the point (-3/2, 1/2), this is calculated as follows:

tangent = y-coordinate / x-coordinate

tangent = (1/2) / (-3/2)

tangent = -1/3

Thus, the value of tangent at the point (-3/2, 1/2) is -1/3, which corresponds to option D.

Answer 2

The value of the tangent at the point
`\((-3/2, 1/2)\) is \(-3\).` Therefore, the correct answer is option A.

Step-by-step explanation:

The tangent of an angle in a right-angled triangle is defined as the ratio of the length of the side opposite the angle to the length of the adjacent side. In this case, we have a point
`\((-3/2, 1/2)\),` which corresponds to a right-angled triangle in the Cartesian plane. The tangent of the angle formed by this point is given by the ratio of the y-coordinate (1/2) to the x-coordinate (-3/2), resulting in a option A. tangent of
`\(-3\).`

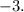
Mathematically, the tangent
`(\( \tan \)) of an angle \( \theta \)` is expressed as
`\( \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \)` . In the given point
`\((-3/2, 1/2)\),` the opposite side is 1/2, and the adjacent side is -3/2. Therefore,
`\( \tan(\theta) = (1/2)/(-3/2) = -3 \).`

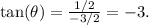
Understanding trigonometric functions and their values is fundamental in geometry and various branches of mathematics. The tangent function, in particular, provides information about the steepness or slope of a line. In this scenario, evaluating the tangent at the given point involves applying the definition of the tangent function and calculating the corresponding ratio of sides in the associated right-angled triangle.