Answer:
The paper is right.
Explanation:
The fraction is
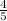 multiplied by
multiplied by
 and the answer is
and the answer is
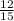 . How did it do that? Well, the numerator (top number),4, was multiplied by the other numerator ,3, which is 12. The same thing with the denominator (bottom number), the denominator,5, was multiplied by the other denominator ,3, which is 15. But as seen in the paper, the fraction
. How did it do that? Well, the numerator (top number),4, was multiplied by the other numerator ,3, which is 12. The same thing with the denominator (bottom number), the denominator,5, was multiplied by the other denominator ,3, which is 15. But as seen in the paper, the fraction