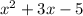Question

The volume of the rectangular prism to the left is represented by the equation V = x ^ 4 + 11x ^ 3 + 34x ^ 2 + 5x - 75 Using what you know about these shapes, whose volumes are calculated using the formula V = lwh find the expression that represents the height (h). Length = x+5, Width = x+3

Answer 1

`h = x^2+3x-5`

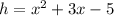
Explanation:

Given

`V = x^4 + 11x^3 + 34x^2 + 5x - 75`

`L = x + 5`

`W = x + 3`

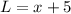
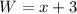
Required

Determine the height (h) of the prism

Volume is calculated as:

`V =lwh`

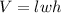
Substitute values for V, l and w

`x^4 + 11x^3 + 34x^2 + 5x - 75 = (x + 5) * (x + 3) * h`

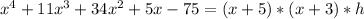
Factorize the expression on the left-hand side

`(x+3)(x^3+8x^2+10x-25)= (x + 5) * (x + 3) * h`

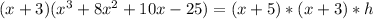
Further, factorize:

`(x+3)(x+5)(x^2+3x-5)= (x + 5) * (x + 3) * h`

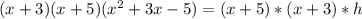
Divide both sides by (x+3)(x+5)

`((x+3)(x+5)(x^2+3x-5))/((x+3)(x+5))= ((x + 5) * (x + 3) * h)/((x+3)(x+5))`

`((x+3)(x+5)(x^2+3x-5))/((x+3)(x+5))= h`

`(x^2+3x-5)= h`

`x^2+3x-5= h`

`h = x^2+3x-5`

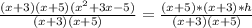
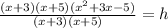
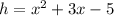
The height of the prism is
`x^2+3x-5`