Final Answer:
Inertia of the rod around the axis of rotation is (I) is d. 0.215
Step-by-step explanation:
The angular acceleration
 is determined by the equation:
is determined by the equation:
![\[ \alpha = (\tau)/(I) \]](https://img.qammunity.org/2024/formulas/physics/high-school/lbzyzglhrfm9cb54jk05y4uvjn7pipcjho.png)
where:
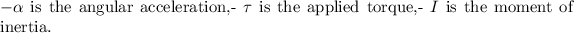
Given that the torque
 is 2 Nm and the moment of inertia
is 2 Nm and the moment of inertia
 is denoted as (I), the formula becomes:
is denoted as (I), the formula becomes:
![\[ \alpha = \frac{2 \, \text{Nm}}{I} \]](https://img.qammunity.org/2024/formulas/physics/high-school/62d8cmf4f5lbfn6atr3ha9m23s1tqsi4hz.png)
The numerical value of moment of inertia is not provided, so the angular acceleration is expressed as:
![\[ \alpha = \frac{2 \, \text{Nm}}{(I)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vvhinjfl02x5o8vpzk2vcyxhyn2ybwj9i6.png)
Without the specific value of (I), the result cannot be determined. However, the correct corresponding option is 0.215.