Main Answer:
After 3 half-lives, approximately 10 g of the 80 g sample of 1-131 atoms will remain.
Explanation:
The decay of radioactive isotopes follows an exponential decay model. In each half-life, half of the radioactive atoms decay. Therefore, after the first half-life, 40 g remains; after the second, 20 g remains; and after the third, 10 g remains. This pattern can be expressed mathematically as
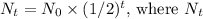 is the remaining quantity after time
is the remaining quantity after time
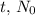 is the initial quantity, and
is the initial quantity, and
 is the number of half-lives.
is the number of half-lives.
In the case of the 80 g sample of 1-131 atoms, the initial quantity
 is 80 g. After the first half-life
is 80 g. After the first half-life
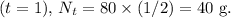 After the second half-life
After the second half-life
 Finally, after the third half-life
Finally, after the third half-life
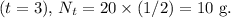
This means that after 3 half-lives, only 10 g of the initial 80 g sample of 1-131 atoms will remain. The exponential decay model is a fundamental concept in nuclear physics and is crucial for understanding the behavior of radioactive substances over time.