Final Answer:
The transformations for the given function
 include a horizontal compression by a factor of
include a horizontal compression by a factor of
 , a horizontal shift to the left by 1 unit, a vertical stretch by a factor of
, a horizontal shift to the left by 1 unit, a vertical stretch by a factor of
 , and a vertical shift downward by 3 units.
, and a vertical shift downward by 3 units.
Step-by-step explanation:
The given function
 can be analyzed to identify the transformations applied to the parent function
can be analyzed to identify the transformations applied to the parent function
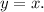 The coefficient of
The coefficient of
 inside the parentheses, 6, represents a horizontal compression by a factor of \(\frac{1}{6}\) since it is the reciprocal of the compression factor. The addition of 1 inside the parentheses causes a horizontal shift to the left by 1 unit. The coefficient of the entire expression,
inside the parentheses, 6, represents a horizontal compression by a factor of \(\frac{1}{6}\) since it is the reciprocal of the compression factor. The addition of 1 inside the parentheses causes a horizontal shift to the left by 1 unit. The coefficient of the entire expression,
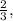 represents a vertical stretch by a factor of
represents a vertical stretch by a factor of
 , and the subtraction of 3 outside the parentheses results in a vertical shift downward by 3 units.
, and the subtraction of 3 outside the parentheses results in a vertical shift downward by 3 units.
Understanding these transformations involves recognizing how each parameter in the function affects the graph's shape and position. The horizontal compression, horizontal shift, vertical stretch, and vertical shift are standard transformations applied to the parent function
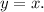 The specific values in this function dictate the extent and direction of these transformations.
The specific values in this function dictate the extent and direction of these transformations.
By breaking down the given function into its components and understanding the impact of each parameter, we can interpret the transformations accurately. In this case, the function undergoes both horizontal and vertical transformations, resulting in a compressed and shifted graph as described in the final answer.