Final Answer:
The minimum weight
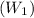 required to hold the block
required to hold the block
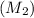 static on the ramp, inclined at 30 degrees with a coefficient of friction (\(\mu\)) of 0.5, is
static on the ramp, inclined at 30 degrees with a coefficient of friction (\(\mu\)) of 0.5, is
Step-by-step explanation:
To determine the minimum weight required
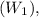 we can use the equation for static equilibrium in the direction perpendicular to the inclined plane. The gravitational force component parallel to the ramp is given by
we can use the equation for static equilibrium in the direction perpendicular to the inclined plane. The gravitational force component parallel to the ramp is given by
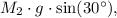 while the friction force opposing motion is
while the friction force opposing motion is
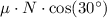 , where
, where
 is the normal force. At the minimum weight
is the normal force. At the minimum weight
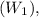 the net force in this direction is zero. Thus, we can set up the equation:
the net force in this direction is zero. Thus, we can set up the equation:
![\[M_2 \cdot g \cdot \sin(30^\circ) = \mu \cdot N \cdot \cos(30^\circ)\]](https://img.qammunity.org/2024/formulas/physics/high-school/ssr2afzkmtiqxklh127vsc74ocb6g3c846.png)
The normal force (\(N\)) is equal to the gravitational force component perpendicular to the ramp, which is
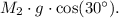 Substituting this into the equation, we get:
Substituting this into the equation, we get:
![\[M_2 \cdot g \cdot \sin(30^\circ) = \mu \cdot M_2 \cdot g \cdot \cos(30^\circ)\]](https://img.qammunity.org/2024/formulas/physics/high-school/vp5109jqz213hlo8rq0ckc4mspdns8h26f.png)
Now, solving for
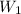 :
:
![\[W_1 = (M_2 \cdot g)/(\sin(30^\circ) + \mu \cdot \cos(30^\circ))\]](https://img.qammunity.org/2024/formulas/physics/high-school/z78s4joni5k5ynmj000ok4x63z23q01od6.png)
This formula gives the minimum weight
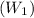 required to hold the block static on the inclined ramp. The calculation involves the gravitational constant
required to hold the block static on the inclined ramp. The calculation involves the gravitational constant
 the mass of the block
the mass of the block
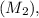 the angle of inclination (30 degrees), and the coefficient of friction
the angle of inclination (30 degrees), and the coefficient of friction
