Answer:
2614 cars will be driven by females, give or take 28.
Explanation:
For each Ford vehicle, there are only two possible outcomes. Either it is driven by a female, or it is not. Cars are independent. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
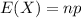
The standard deviation of the binomial distribution is:

Company determined that the probability of a randomly selected Ford vehicle on the road being driven by a female is 0.71.
This means that
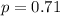
If there are 3,682 Ford vehicles in your town
This means that

__________ cars will be driven by females, give or take __________.
The mean and the standard deviation complete this. So
Mean:
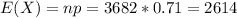
Standard deviation:

2614 cars will be driven by females, give or take 28.