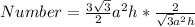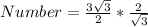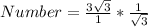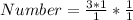Answer:
3 of the pyramids
Explanation:
Given:
Hexagonal Prism
Hexagonal based pyramid
Required
How many of the pyramid will fill up the prism
To do this, we start by calculating the volumes of both shapes.
Let V1 be the volume of the hexagonal prism
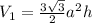
Where: a = base and h = height
Let V2 be the volume of the hexagonal based pyramid
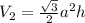
Where: a = base and h = height
The number of the pyramid that can occupy the prism is calculated by dividing V1 by V2
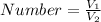
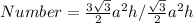
Convert division to multiplication