Question

You have been handed an unknown battery. Using your multimeter, you determine that when a 4.30 resistor is connected across the battery's terminals, the current in the battery is 0.500 A. When this resistor is replaced by an 9.4 resistor, the current drops to 0.250 A. From those data, find the emf and internal resistance of your battery.

Answer 1

Ri = 0.8 Ω

V= 2.55 V

Step-by-step explanation:

• Since the internal resistance of the battery is connected in series with the resistor connected across the battery's terminals, applying Ohm's Law, we can write the following equation, when R₁=4.30 Ω, and I₁=0.500A:

`I_(1) = (V)/(R_(i) + 4.3 \Omega ) = 0.500 A (1)`

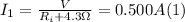
• We can apply exactly this same expression, when R₂ = 9.4Ω, and I₂ = 0.250A:

`I_(2) = (V)/(R_(i) + 9.4 \Omega) } = 0.250 A (2)`

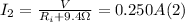
• Now, we can divide (1) by (2) as follows:

`(R_(i) + 9.4 \Omega)/(R_(i) + 4.3 \Omega) = (I_(1) )/(I_(2)) = 2 (3)`

• Solving for Ri, we get Ri = 0.8 Ω
• Replacing this value in (1) we can solve for V, as follows:
• V = I₁ * (Ri + R₁) = 0.500 A * (0.8Ω + 4.3Ω) = 2.55 V

⇒ V = 2.55 V (emf of the battery)