Answer:
the cart's speed at point B is 15.72 ft/s
Step-by-step explanation:
Given the data in the question;
The car travels from point A to C in 3.00 s, its average acceleration
 will be;
will be;
 = [
= [
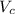 -
-
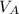 ] / Δt
] / Δt
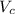 is 17.4 ft/s,
is 17.4 ft/s,
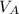 is 13.2 ft/s and Δt is 3.00 s
is 13.2 ft/s and Δt is 3.00 s
so we substitute
 = [17.4 - 13.2] / 3
= [17.4 - 13.2] / 3
 = 4.2 / 3
= 4.2 / 3
 = 1.4 ft/s²
= 1.4 ft/s²
so average acceleration of the cart between the points A and B is 1.4 ft/s²
The instantaneous value of the velocity of the cart at point B will be;
 = Δv / Δt
= Δv / Δt
now substitute [
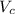 -
-
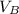 ] for Δv and t' for Δt
] for Δv and t' for Δt
 = [
= [
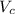 -
-
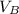 ] / t'
] / t'
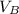 =
=
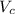 -
-
 ( t' )
( t' )
so we substitute 17.4 ft/s for
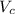 , 1.20 s for t' and
, 1.20 s for t' and
 = 1.4 ft/s²
= 1.4 ft/s²
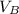 = 17.4 - (1.4 × 1.20)
= 17.4 - (1.4 × 1.20)
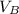 = 17.4 - 1.68
= 17.4 - 1.68
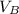 = 15.72 ft/s
= 15.72 ft/s
Therefore, the cart's speed at point B is 15.72 ft/s