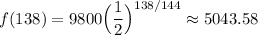Question

PLS HELP TIMED QUESTION!!!

A quantity with an initial value of 9800 decays exponentially at a rate such that the quantity cuts in half every 6 days. What is the value of the quantity after 138 hours, to the nearest hundredth?

Answer 1

About 5043.58

Explanation:

The standard form for an exponential decay after t time is:

`\displaystyle f(t)=a(r)^(t/d)`

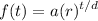
Where a is the initial value, r is the rate decay, t is the time that has passed, and d is the amount of time it takes for 1 cycle.

The initial value is 9800. So a = 9800.

The quantity cuts in half. So, r = 1/2.

And it cuts in half every 6 days. For this question, we will convert this to hours. 6 days = 144 hours. So, we can let d = 144, where t will be in hours.

Therefore, our function is:

`\displaystyle f(t)=9800\Big((1)/(2)\Big)^(t/144)`

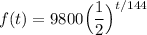
Where t is the amount of time that has passed, in hours.

Then the quantity left after 138 hours will be:

`\displaystyle f(138)=9800\Big((1)/(2)\Big)^(138/144)\approx 5043.58`