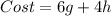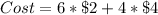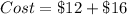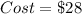Answer:
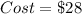
Explanation:
Given
Represent Goldfish with g and hermit crabs with h.
The first statement, we have:
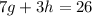
The second statement, we have:
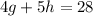
Required
Determine the selling price of 6 goldfish and 4 hermit crabs
The equations are:
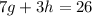 --- (1)
--- (1)
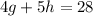 --- (2)
--- (2)
Make g the subject in (2)
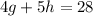
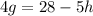
Divide both sides by 4
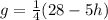
Substitute
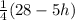 for g in (1)
for g in (1)
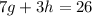
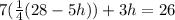

Multiply through by 4
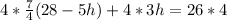
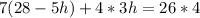
Open bracket
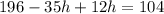
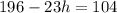
Collect Like Terms

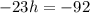
Make h the subject

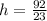
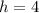
Substitute 4 for h in
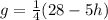
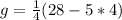

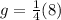

This implies that:
1 goldfish = $2
1 hermit crab = $4
The cost of 6 goldfish and 4 hermit crabs is: