Question

A restaurant serves hot chocolate that has a mean temperature of 175 degrees with a standard deviation of 8.1 degrees. Find the probability that a randomly selected cup of hot chocolate would have a temperature of less than 161 degrees. Would this outcome warrant a replacement cup (meaning that it would be unusual)

Answer 1

Answer: The probability that a randomly selected cup of hot chocolate would have a temperature of less than 161 degrees =0.042

This outcome would warrant a replacement cup.

Explanation:

Let x be a random variable that represents the temperature of hot chocolates.

GIven: Mean temperature = 175 degrees

standard deviation = 8.1 degrees

The probability that a randomly selected cup of hot chocolate would have a temperature of less than 161 degrees =
`P(x<161)`

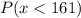
`=P((x-\mu)/(\sigma)<(161-175)/(8.1))\\\\=P(Z<-1.7284) [Z=(x-\mu)/(\sigma)]\\\\=1-P(Z<1.7284)\\\\=1-0.9580\\\\=0.042`

Hence, the probability that a randomly selected cup of hot chocolate would have a temperature of less than 161 degrees =0.042 < 0.5 (unusual)

i.e. this outcome would warrant a replacement cup.