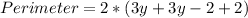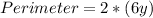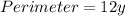Answer:
Explanation:
Given
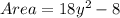 -- two rectangles
-- two rectangles
Required
Determine the perimeter of one of the rectangles
First, calculate the area (A) of 1 rectangle

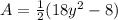

Express as difference of two squares
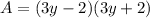
Area is calculated as:

So, by comparison:

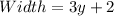
The perimeter is:
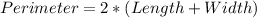
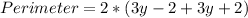
Collect Like Terms