Answer:
Surface area of the right prism =
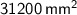
Explanation:
To calculate the surface area of a right prism with an isosceles triangle as a base, we need to find the areas of the lateral faces and the base.
The surface area
 of a right prism is given by the formula:
of a right prism is given by the formula:
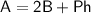
where:
-
 is the area of the base,
is the area of the base,
-
 is the perimeter of the base, and
is the perimeter of the base, and
-
 is the height of the prism.
is the height of the prism.
For a right prism with an isosceles triangle as the base, the area
 of the base can be found using Heron's formula, which is given by:
of the base can be found using Heron's formula, which is given by:
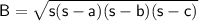
where
 is the semi-perimeter of the triangle, and
is the semi-perimeter of the triangle, and
 and
and
 are the lengths of the triangle sides.
are the lengths of the triangle sides.
The semi-perimeter
 is calculated as:
is calculated as:
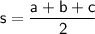
Given that the sides of the isosceles triangle are 50mm, 50mm, and 80mm, we can calculate
 as:
as:
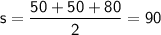
Now, we can find the area
 using Heron's formula:
using Heron's formula:
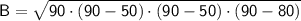

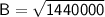
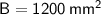
Next, calculate the perimeter
 of the base:
of the base:
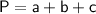
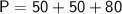
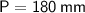
Now, substitute these values into the formula for the surface area:
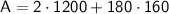
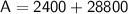
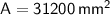
Therefore, the surface area of the right prism is
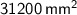 .
.