Question

Given the rectangular prism

1) determine the height

2) calculate the area of the bottom base/face

3) the rectangular prism has a volume of 1200 cm (cubed). How many kilometers of water can the prism hold?

Answer 1

1) 15 cm

- To determine the height, let’s do the Pythagorean Theorem,
`a^(2) + b^(2) = c^(2)`.
- Let’s input it now!
`8^(2) + b^(2) = 17^(2)`
- Plug it into a calculator.
`64 + b^(2) = 289`
- Change the format.
`289 - 64 = b^(2)`
- Simplify.
`225 = b^(2)`
- Take the square root.
`√(225) = 15`

2) 80 squared cm

- Let’s use the formula, bh (base × height)
- 10 × 8 = 80

3) 1.2 × 10 to the power of -12 km³

- There are 1 billion cm³ in a km³, so 1200/1 billion would be 1.2 × 10 to the power of -12

—————

Please remember to revise this and make it in your own words if you want! I hope this helps you. -Doodle

—————

Answer 2

1) height = 15cm

2) Base Area = 80cm²

3)
`\sf 1.2 * 10^(-12)` cubic kilometers

Explanation:

Let's address each part of the question:

1) Determine the height:

For the rectangle face, we can use the Pythagorean theorem since we know the diagonal (
`\sf 17\, \textsf{cm}`) and one side (
`\sf 8\, \textsf{cm}`). Let
`\sf h` be the height.

`\sf h = \sqrt{\textsf{diagonal}^2 - \textsf{length}^2}`

`\sf h = √(17^2 - 8^2) \, \textsf{cm}`

`\sf h = √(289 - 64) \, \textsf{cm}`

`\sf h = √(225) \, \textsf{cm}`

`\sf h = 15 \, \textsf{cm}`

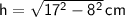
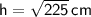
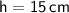
So, the height of the rectangular prism is
`\sf 15\, \textsf{cm}`.

`\hrulefill`

2) Calculate the area of the bottom base/face:

For the bottom base, the area (
`\sf A_{\textsf{base}}`) is given by the product of the length and width.

`\sf A_{\textsf{base}} = \textsf{length} * \textsf{width}`

`\sf A_{\textsf{base}} = 10 * 8 \, \textsf{cm}^2`

`\sf A_{\textsf{base}} = 80 \, \textsf{cm}^2`

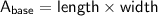
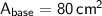
So, the area of buttom base/face = 80 cm².

`\hrulefill`

3) Calculate the volume of the rectangular prism and convert to kilometers cubed:

Given that the volume (
`\sf V`) is
`\sf 1200\, \textsf{cm}^3`, to convert this volume to kilometers cubed, we divide by
`\sf 1,000,000,000,000` (since there are
`\sf 1,000,000,000,000` cubic centimeters in a cubic kilometer).

`\sf V_{\textsf{kilometers}^3} = (1200)/(1,000,000,000,000) \, \textsf{kilometers}^3`

`\sf V_{\textsf{kilometers}^3} = 1.2 * 10^(-12) \, \textsf{kilometers}^3`

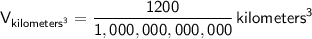
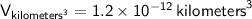
So, the rectangular prism can hold
`\sf 1.2 * 10^(-12)` cubic kilometers of water.